10.11

2017-01-08

(a)

スポットレート spot rate, s

s = (0.070, 0.073, 0.077, 0.081, 0.084, 0.088)

フォワード・レート forward rate, f

f_0,1 = s₁ = 0.070
f_1,2 = (1+s₂)²/(1+s₁)¹-1 = 1.073²/1.070¹-1 = 0.076
f_2,3 = (1+s₃)³/(1+s₂)²-1 = 1.077³/1.073²-1 = 0.085
f_3,4 = (1+s₄)⁴/(1+s₃)³-1 = 1.081⁴/1.077³-1 = 0.093
f_4,5 = (1+s₅)⁵/(1+s₄)⁴-1 = 1.084⁵/1.081⁴-1 = 0.096
f_5,6 = (1+s₆)⁶/(1+s₅)⁵-1 = 1.088⁶/1.084⁵-1 = 0.108

支払利息のキャッシュフロー cash flow, x
想定元本 A = 1000(unit 1000$)

x1 = A f0,1 = 1000×0.070 =  70
x2 = A f1,2 = 1000×0.076 =  76
x3 = A f2,3 = 1000×0.085 =  85
x4 = A f3,4 = 1000×0.093 =  93
x5 = A f4,5 = 1000×0.096 =  96
x6 = A f5,6 = 1000×0.108 = 108

割引係数 discount factor, d

d1 = 1/(1+s1)1 = 1/1.0701 = 0.935
d2 = 1/(1+s2)2 = 1/1.0732 = 0.869
d3 = 1/(1+s3)3 = 1/1.0773 = 0.800
d4 = 1/(1+s4)4 = 1/1.0814 = 0.732
d5 = 1/(1+s5)5 = 1/1.0845 = 0.668
d6 = 1/(1+s6)6 = 1/1.0886 = 0.603

変動金利の現在価値 present value, PV₁

PV₁ = x₁d₁ + x₂d₂ + x₃d₃ + x₄d₄ + x₅d₅ + x₆d₆
= 70 × 0.935 + 76 × 0.869 + 85 × 0.800 + 93 × 0.732 + 96 × 0.668 + 108 × 0.603
= 65.5 + 66.0 + 68.0 + 69.0 + 64.1 + 65.1
= 396.7 (1000$)

(b)

固定金利を r と置く。

固定金利のキャッシュフロー cash flow, y

y_i = Ar, i=1,2,...,6.

固定金利の割引係数 discount factor, d

d_i = 1/(1+r)ⁱ, i=1,2...,6.

固定金利の現在価値 present value, PV₂

PV₂ = Σy_id_i, i=1,2...,6.

スワップの変動側と固定側の価値が等しい固定側の金利 r は、 次式を満たす。

PV₂ - PV₁ = 0

すなわち、

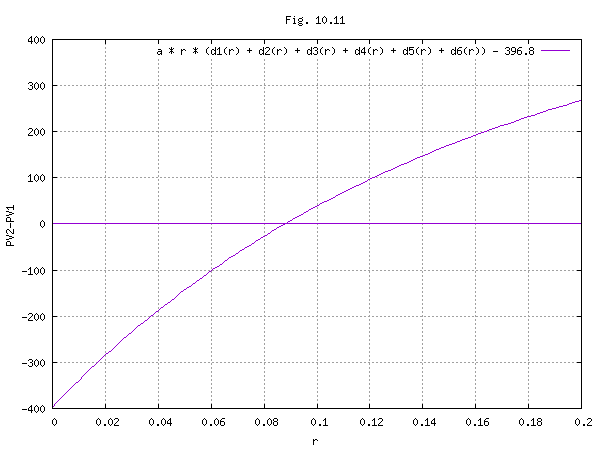
1000r[ 1 / (1 + r)¹ + 1 / (1 + r)² + 1 / (1 + r)³ + 1 / (1 + r)⁴ + 1 / (1 + r)⁵ + 1 / (1 + r)⁶ ] - 396.7 = 0 (1)

(1)式を図化すると下図となる。

(1)式をrについて解くと、r = 0.088 である。

図化ファイル

10.11.plt for gnuplot

Python

2016-10-23 10.11.py

JavaScript

2024-11-03 10.11.js

Gauche

2024-11-03 10.11.scm

Julia

2024-11-03 10.11.jl

Fortran

2024-11-03 10.11.f90

history

2016-10-22 created.
2016-10-23 typo fixed and python code added.
2017-01-08 typo fixed.
2021-02-19 change XHTML to html5, change shift-jis to utf-8, add viewport.
2024-11-03 add a JavaScript code, a Gauche code, a Julia code and a Fortran code.