contents

10.3

2016-12-30

r の推定方法

先渡価格の理論値と実値との差の二乗の和が最小になる初期現物価格 s と金利 r を求めることにより、金利 r を推定する。

4月初めにおける、4月末、7月末、9月末、12月末の先渡価格の実値をそれぞれ、 

fapr = 406.50(¢)
fjul = 416.64(¢)
fsep = 423.48(¢)
fdec = 433.84(¢)
と置く。

先渡価格の理論値を

f = s / d(0,M) + ∑c(k) / d(k,M), k = 0...M-1.
と置く。

割引係数d(k, M)は、年当たりm期間複利で計算する(m=12)。金利rは一定とする。 

d(k, M) = 1 / (1 + r / m)M - k

4月末、7月末、9月末、12月末の先渡価格の理論値を表わす関数は、それぞれ 

f4(s,r) = s(1+r/12)1 + c[(1+r/12)1]
f7(s,r) = s(1+r/12)4 + c[(1+r/12)4+(1+r/12)3+...+(1+r/12)1] 
f9(s,r) = s(1+r/12)6 + c[(1+r/12)6+(1+r/12)5+...+(1+r/12)1] 
f12(s,r) = s(1+r/12)9 + c[(1+r/12)9+(1+r/12)8+...+(1+r/12)1]
である(2016-10-16 訂正)。 ただし、月当たり保有費用c(k)=c=20/12(¢)である。

4月末、7月末、9月末、12月末の先渡価格の理論値と実値との差の二乗の和を

g(s,r) = (f4(s,r)-fapr)2+(f7(s,r)-fjul)2+(f9(s,r)-fsep)2+(f12(s,r)-fdec)2
と置き、g(s, r) が最小になる r を求める。

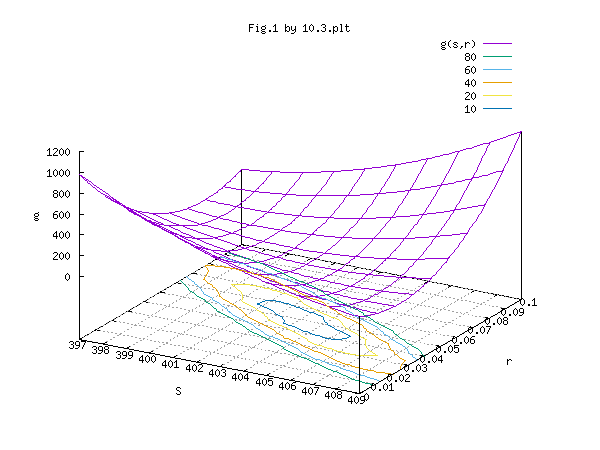
x軸をs、y軸をr、z軸を g(s, r) として、y = g(s, r)を図化すると、次図(Fig.1)になる。
xy平面上の曲線は、g(s, r)の値の等高線である。
等高線から、求める s と r は、それぞれ、403 と 0.05 の付近にある。
graph of g(s,r)

y = g(s, r)が最小となるsとrを求める方法

s = 402.1435, ... , 403.1436. (刻みΔsは0.000001、個数は100)
r = 0.050022, ... , 0.050023. (刻みΔrは0.00000001 = 1*10-8、個数は100)
上記のsとrの組み合わせ全てに対して、g(s, r)を計算する。
計算したg(s, r)から、次の条件1)を満たすs0, r0, g(s0, r0)を探し、 そのr0を解答とする。

  1. 計算したg(s, r)のなかで、g(s0, r0)が最小である。
  2. s0 と r0 が、それぞれ s と r の境界点にない。
  3. gの全ての偏微分が0、すなわち、
    ∂g/∂s = 0
    ∂g/∂r = 0

プログラムを作るにあたっては、上記の c. は次の条件に置き換える。 

Δg/Δs = |(g(s0+Δs,r0)-g(s0,r0))/((s0+Δs)-(s0))| < eps
Δg/Δr = |(g(s0,r0+Δr)-g(s0,r0))/((r0+Δr)-(r0))| < eps
ただし、eps = 1/100とする。

1) テキスト、p.607、B.3 最適化 １必要条件

rの推定結果

備考のプログラムから求めた、s0、r0、g(s0,r0)は、それぞれ、 


403.143523
  0.05002238
  0.00002459
である。

よって、金利rの推定値は、0.050である。
（この推定値は、テキストの解答「5%」に一致する。）

図化コマンド

Fig.1は、GNUPLOTで作成した。図化コマンドは、次のリンクに示す。

10.3.plt

g(s, r)の最小値を探すプログラム

上記の (s, r) の全組 (si, rj)(100 × 100 = 10000組)に対して g(s, r) を計算し、 g(s, r) の最小値を探すプログラムを次のリンクに示す。

10.3.py

history

created on 2011-08-28, revised on 2011-10-04, 2011-10-08, 2011-10-19, 2016-10-16.
2016-10-16 forward price functions corrected and Python code added, Fortran code removed.
2016-11-06 Maxima solution added.
2016-12-30 Maxima solution moved to 10.3e.html
2021-02-18 change XHTML to html5, change shift-jis to utf-8, add viewport.

contents