2016-12-24

10.3、別解2

解法

先渡価格の理論値と実値との差の二乗の和が最小になる初期現物価格Sと金利rを最大傾斜法(the mothod of steepest descent)で求める。

解

最大傾斜法により得られた解は、

s = 403.14
r = 0.0500

収束条件は、次とした。

∂g/∂s = Δg/Δs = g(s+Δs, r) / Δs < 0.01
∂g/∂r = Δg/Δr = g(s, r+Δr) / Δr < 0.1

Δs = 0.000001=1e-6
Δr = 0.0000001=1e-7

最大傾斜法の収束の状況

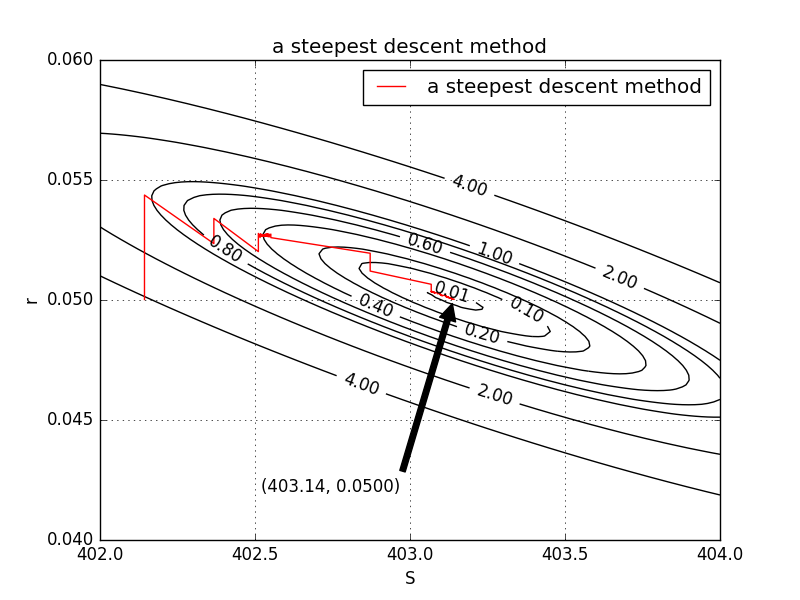
最大傾斜法の収束の状況を下図に示す。

code

繰り返し式は、次式とした。

x_n+1 = x_n + α_np_n

• α_n は、二乗和g(x_n+αp_n)を最小とするスカラー(scalar)。codeでは、α_n=j*αとしてα_nを探索した。。
  
• 点 x_n = (s_n, r_n)
  
• 方向ベクトルp(the direction vector)は、gの傾斜の負とした。codeでは、傾斜の各方向の値をΔg/Δrの絶対値で除した値を用いた。
  p = (-∂g/∂s, -∂g/∂r) / |∂g/∂r|
  = (-(Δg/Δs)/|Δg/Δr|, -(Δg/Δr)/|Δg/Δr|)

# 10.3c.py
# 2016/12/24
#
# gradient descent, steepest descent 
#
# maxima's answer
# s = 403.1435406698565
# r = 0.05002238137869293
#
# this code answer
# i = 4138
# s = 403.142
# r =   0.0500

import numpy as np
import matplotlib.pyplot as plt
import math

def g(s, r):
  d1 = 1 / (1 + r / m)
  d2 = 1 / (1 + r / m) ** 2
  d3 = 1 / (1 + r / m) ** 3
  d4 = 1 / (1 + r / m) ** 4
  d5 = 1 / (1 + r / m) ** 5
  d6 = 1 / (1 + r / m) ** 6
  d7 = 1 / (1 + r / m) ** 7
  d8 = 1 / (1 + r / m) ** 8
  d9 = 1 / (1 + r / m) ** 9
  f4  = s / d1 + c /d1
  f7  = s / d4 + c * (1/d4 + 1/d3 + 1/d2 + 1/d1)
  f9  = s / d6 + c * (1/d6 + 1/d5 + 1/d4 + 1/d3 + 1/d2 + 1/d1)
  f12 = s / d9 + c * (1/d9 + 1/d8 + 1/d7 + 1/d6 + 1/d5 + 1/d4 + 1/d3 + 1/d2 + 1/d1)
  a = np.array([(f4 - fapr), (f7 - fjul), (f9 - fsep), (f12 - fdec)])
  g = sum(a ** 2)
  return g

# main

# inpput
m = 12
c = 20.0 / m
fapr = 406.50
fjul = 416.64
fsep = 423.48
fdec = 433.84

s  = 402.1435
ds =   0.000001

r  = 0.05002
dr = 0.0000001

alpha = 1e-6

# calculate
ss = [s]
rr = [r]

fmt1='{:10.5f}{:10.6f}{:10.5f}'

imax = 100000
fmt2='{}{:7d}{:8.3f}{:7.4f}{:5.2f}{:7.3f}{:6.2f}{:7.3f}{:7.4f}'
for i in range(imax):
  gsr  = g(s, r)
  dgds = (g(s + ds, r)      - gsr) / ds
  dgdr = (g(s,      r + dr) - gsr) / dr

  if (abs(dgds) < 0.01 and abs(dgdr) <0.1):
    ss.append(s)
    rr.append(r)
    print(fmt2.format('i,s,r,gsr,dgds,dgdr,ps,pr',i,s,r,gsr,dgds,dgdr,p_s,p_r))
    print('dgds < 0.01, dgdr <0.1')
    break

  p_s = -dgds / abs(dgdr)
  p_r = -dgdr / abs(dgdr)

  if abs(dgds) < 0.1 and abs(dgdr) < 0.1:
    alpha = 1e-8
  else:
    alpha = 1e-7

  j = 0
  while 1:
    if  g(s + (j+1) * alpha * p_s, r + (j+1) * alpha * p_r) \
      < g(s +  j    * alpha * p_s, r +  j    * alpha * p_r):
      j = j + 1
    else:
      break

  s = s + j * alpha * p_s
  r = r + j * alpha * p_r

  if (i % 1000) ==0:
    print(fmt2.format('i,s,r,gsr,dgds,dgdr,ps,pr', \
                       i, s, r, gsr,dgds, dgdr, p_s, p_r))
    ss.append(s)
    rr.append(r)

  ss.append(s)
  rr.append(r)


# plot contour and a descent method path

sstart, send, sstep = 402.0,  404.0,  1e-6
rstart, rend, rstep =   0.04,   0.06, 1e-8

xs     = np.linspace(sstart, send, 100)
yr     = np.linspace(rstart, rend, 100)
xx, yy = np.meshgrid(xs, yr)
zz     = g(xx, yy)

plt.title('a steepest descent method')
plt.xlabel('S')
plt.ylabel('r')
plt.grid()
plt.annotate('(403.14, 0.0500)', \
           xy=(403.14, 0.0500),  \
       xytext=(402.52 , 0.042) , \
   arrowprops = dict(facecolor = 'black', shrink = 0.02))
cont = plt.contour(xx, yy, zz, colors = 'k', \
       levels = [0.01, 0.1, 0.2, 0.4, 0.6, 0.8, 1, 2, 4])
cont.clabel(fmt='%.2f', fontsize=12)
plt.plot(ss, rr, 'r', label = 'a steepest descent method')
plt.axis([402,404,0.04,0.06])
plt.legend()
plt.show()
# eof

最大傾斜法(the method of steepest descent)について

最大傾斜法のcodeは、次を見て作成した。

David G. Luenberger, Optimization by Vector Space Methods, John Wiley & Sons, Inc., 1969, p.285.

history

2016-12-24 create.
2021-02-19 change XHTML to html5, change shift-jis to utf-8, add viewport.