2.11 Conflicting recommendations

(条件)r = 0.05
プロジェクト1とプロジェクト2の正味現在価値をそれぞれNPV₁、 NPV₂とすると、それぞれは次となる。

NPV₁ = -100 + 30 / (1 + r) + ... + 30 / (1 + r)⁵
= -100 + (30 / r)(1 - 1 / (1 + r)⁵)
= 29.88
NPV₂ = -150 + 42 / (1 + r) + ... + 42 / (1 + r)⁵
= -150 + (42 / r)(1 - 1 / (1 + r)⁵)
= 31.48
= 31.84

∴正味現在価値基準からは、プロジェクト2が推奨案となる。

プロジェクト1の内部収益率IRR₁は、 次式を満たすcをIRR=(1/c)-1の関係に代入して得る。

f(c)=-100 + 30c + 30c² + 30c³ + 30c⁴ + 30c⁵ = 0

f(c)の図をFig.2.11.1に示す。

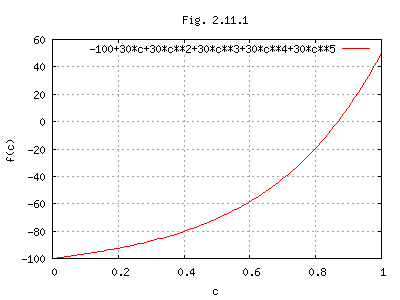
試行錯誤により、c = 0.868

IRR₁ = (1 / c) - 1 = 0.152 = 15.2(%)

プロジェクト1の内部収益率IRR₂は同様に、

g(c) = -150 + 42c + 42c² + 42c³ + 42c⁴ + 42c⁵ = 0

g(c)の図をFig. 2.11.2に示す。

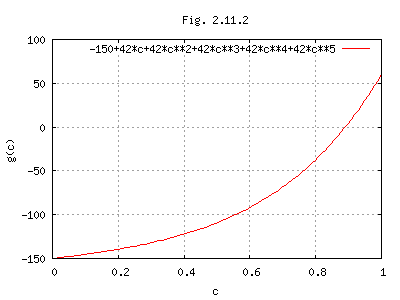
試行錯誤により、 c = 0.891 0.890
IRR₂ = (1 / c) - 1 = 0.122 0.124 = 12.2 12.4 (%)
∴内部収益率基準からは、プロジェクト1が推奨案となる。

上に示す通り、内部収益率と正味現在価値では異なる推奨案が求まった。 その理由を次に示す。(added on 2016-12-04.)

内部収益率はキャッシュフロー流列で定まるが、 キャッシュフロー流列の正味現在価値はキャッシュフロー流列と金利で定まるため、 推奨案が異なる場合がある。

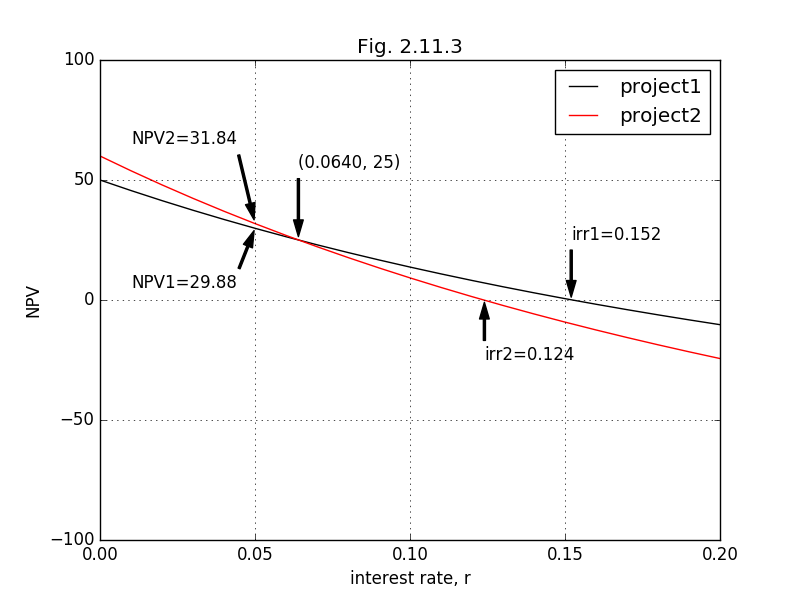
下図で言うと、NPVが等しくなる金利を超える場合(r > 0.0640)プロジェクト1がNPV基準 と内部収益率基準で推奨案となるが、NPVが等しくなる金利未満(r < 0.0640)では、 NPV基準ではプロジェクト2が推奨案になり、内部収益率基準ではプロジェクト1 が推奨案になる。

下図の説明
プロジェクト1とプロジェクト2の金利とNPVの関係をFig. 2.11.3 に示す。 irr1、irr2は、プロジェクト1とプロジェクト2の内部収益率を表す。 (0.0640, 25)は、プロジェクト1のNPVとプロジェクト2のNPVが等しくなる金利 (r = 0.0640)とそのNPV(= 25)を表す。

上の図を書くcode を次に示す。

# 2.11.plot.py
# create on 2016/12/04

import numpy
import matplotlib.pyplot as plt

# input
step = 0.01
rate = numpy.arange(0, 1, step)
cfs1 = numpy.array([-100, 30, 30, 30, 30, 30])
cfs2 = numpy.array([-150, 42, 42, 42, 42, 42])

# calculate
npv1 = numpy.array([numpy.npv(x, cfs1) for x in rate])
npv2 = numpy.array([numpy.npv(x, cfs2) for x in rate])

# output
plt.title('Fig. 2.11.3')
plt.xlabel('interest rate, r')
plt.ylabel('NPV')
plt.axis([0, 0.2, -100, 100])
plt.grid(True)
plt.plot(rate, npv1, 'k', label = 'project1')
plt.plot(rate, npv2, 'r', label = 'project2')
plt.legend()
w  = 1.5
hw = 7
fc = 'black'
plt.annotate('(0.0640, 25)', xy = (0.0640, 25), xytext = (0.0640, 55), \
             arrowprops = dict(width = w, headwidth = hw, facecolor = fc, \
             shrink = 0.05))
plt.annotate('irr2=0.124',  xy = (0.124, 0), xytext = (0.124, -25), \
             arrowprops = dict(width = w, headwidth = hw, facecolor = fc, \
             shrink = 0.05))
plt.annotate('irr1=0.152',  xy=(0.152,   0), xytext = (0.152,  25), \
             arrowprops = dict(width = w, headwidth = hw, facecolor = fc, \
             shrink = 0.05))
plt.annotate('NPV1=29.88', xy = (0.05, 29.88), xytext = (0.01, 5), \
             arrowprops = dict(width = w, headwidth = hw, facecolor = fc, \
             shrink = 0.05))
plt.annotate('NPV2=31.84', xy = (0.05, 31.84), xytext = (0.01, 65), \
             arrowprops = dict(width = w, headwidth = hw, facecolor = fc, \
             shrink=0.05))
plt.show()
# end

備考 f(c)=0を解く

Python

code

# 2.11a.py
# 22:03 2015-04-02

def f(c):
  x=[-100,30,30,30,30,30]
  cc=[1,c,c**2,c**3,c**4,c**5]
  return sum(map(lambda x,y: x*y,x,cc))

i=1
eps=1e-3
left=0
right=1
mid=(left+right)/2
while abs(f(mid))>eps:
  if(f(mid)>0):
    right=mid
  else:
    left=mid
  mid=(left+right)/2
  i=i+1

c=mid
irr=1/c-1

print("c=    ",round(c,2))
print("f(c)= {:.2e}".format(f(c)))
print("i=    ",i)
print("irr=1/c-1=",round(irr,2))
# end

output

c=     0.87
f(c)= -6.04e-05
i=     15
irr=1/c-1= 0.15

Fortran

f(c)=0を解くFortranのコードを次に示す。

2.11a.f90

Gauche

f(c)=0を解くGaucheのコードを次に示す。

2.11a.scm

備考 g(c)=0を解く

Python

code

# 2.11b.py
# 22:13 2015-04-02

def f(c):
  x=[-150,42,42,42,42,42]
  cc=[1,c,c**2,c**3,c**4,c**5]
  return sum(map(lambda x,y: x*y,x,cc))

i=1
eps=1e-5
left=0
right=1
mid=(left+right)/2
while abs(f(mid))>eps:
  if(f(mid)>0):
    right=mid
  else:
    left=mid
  mid=(left+right)/2
  i=i+1

c=mid
irr=1/c-1

print("c=    ",round(c,2))
print("f(c)= {:.2e}".format(f(c)))
print("i=    ",i)
print("irr=1/c-1=",round(irr,2))
# end

output

c=     0.89
f(c)= 6.24e-07
i=     25
irr=1/c-1= 0.12

Fortran

g(c)=0を解くFortranのコードを次に示す。

2.11b.f90

Gauche

g(c)=0を解くGaucheのコードを次に示す。

2.11b.scm

Python code with numpy.npv() and numpy.irr()

code

numpyの関数npv(), irr()を用いたcodeを次に示す。(added on 2016-12-04.)

# 2.11.numpy.npv.py
# created on 2016/12/03
# $Id: 2.11.html 1.11 2021/02/14 06:57:39 s Exp $

import numpy

# input
rate = 0.05
cfs1 = [-100, 30, 30, 30, 30, 30]
cfs2 = [-150, 42, 42, 42, 42, 42]

# calculate
n1 = numpy.npv(rate, cfs1)
n2 = numpy.npv(rate, cfs2) 
i1 = numpy.irr(cfs1)
i2 = numpy.irr(cfs2)

# output
print('npv1=', round(n1, 2))
print('npv2=', round(n2, 2))
print('irr1=', round(i1, 3))
print('irr2=', round(i2, 3))

# end

output

npv1= 29.88
npv2= 31.84
irr1= 0.152
irr2= 0.124

備考 図化コマンド

図化コマンドを次のリンクに示す。(2011-10-26)

• Fig.2.11.1
• Fig.2.11.2

history

2004-4-10, revised on 2004-05-01, 2007-04-21, 2011-10-26, 2011-11-02, 2014-02-15, 2015-04-02, 2016-09-28.
2016-09-28 Fortran, Gauche, Javascript codes moved to links.
2016-12-04 code with numpy.npv(), numpy.irr() added. explanation for different recommendations added.
2021-02-11 change to html5, utf-8. add viewport.
2021-02-14 move history.