2.13

(a)

P(c)=P_x(c)-P_y(c)
と置くと、
P(c)=(x₀-y₀)+(x₁-y₁)c+...+(x_n-y_n)cⁿ
∴P(0)=x₀-y₀ < 0
∴P(1)=(x₀-y₀)+(x₁-y₁)+...+(x_n-y_n) = ∑(x_i-y_i) > 0
上記2式から、交差値c>0がある。

(b)

2005-7-3更新, 2006-11-19更新, 2007-04-21更新
-100+30c+30c²+...+30c⁵=-150+42c+42c²+...+42c⁵
0=-50+12c+12c²+...+12c⁵
上式の右辺をFig.2.13bに示す。(2006-11-19)
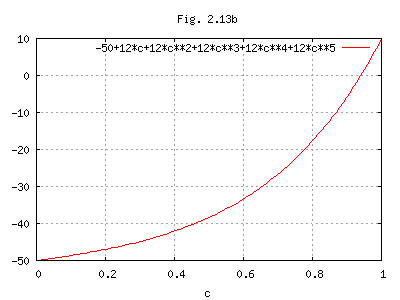
graph
二分法で解く(備考参照)と、
c=0.9398
となる。

備考

Python

code


# 2.13.py
# 22:27 2015-04-02

def f(c):
  x=[-50,12,12,12,12,12]
  cc=[1,c,c**2,c**3,c**4,c**5]
  return sum(map(lambda x,y: x*y, x,cc))

i=1
eps=1e-3
left=0
right=1
mid=(left+right)/2

while abs(f(mid))>eps:
  if(f(mid)>0):
    right=mid
  else:
    left=mid
  mid=(left+right)/2
  i=i+1

c=mid
irr=1/c-1

print("c=    ",round(c,2))
print("f(c)= {:.2e}".format(f(c)))
print("i=    ",i)
# end

output


c=     0.94
f(c)= 7.29e-04
i=     16

Fortran

0=-50+12c+12c²+...+12c⁵を2分法で解くFortranのコードを次に示す。

2.13.f90

Gauche

0=-50+12c+12c²+...+12c⁵を2分法で解くGaucheのコードを次に示す。

2.13.scm

GNUPLOT

(2006-11-19)
Fig.2.13bは、次のソフトで作成した。

        G N U P L O T
        Version 4.0 patchlevel 0
        last modified Thu Apr 15 14:44:22 CEST 2004
        System: FreeBSD 6.1-RELEASE-p10

        Copyright (C) 1986 - 1993, 1998, 2004
        Thomas Williams, Colin Kelley and many others

Fig.2.13bを作成したスクリプトファイルは、次のとおりです。

2.13b.plt

history

2005-7-2, revised on 2011-11-02, 2011-11-03, 2014-02-15, 2016-09-28.
2016-09-28 Fortran, Gauche, Javascript codes moved to linked files.
2021-02-11 change to html5, utf-8. add viewport.
2021-02-14 move history.