2.14
想定金利を r と置く。
資産の価格を 100 ($)と仮定する。
減価償却率1 = (25%, 38%, 37%)
減価償却率2 = (100/3%, 100/3%, 100/3%)
減価償却率1のキャッシュフロー = (25, 38, 37)
減価償却率1のキャッシュフロー = (100/3, 100/3, 100/3)
減価償却率1の現在価値 PV1 = 25 / (1 + r) + 38 / (1 + r)2 + 37 / (1 + r)3
減価償却率2の現在価値PV2 = 100 / 3 / (1 + r) + 100 / 3 / (1 + r)2 + 100 / 3 / (1 + r)3
PV2 - PV1 ≥0, r ≥ 0
∴ 減価償却の現在価値を最大にしたい場合は、後者(PV2)の方法が
望ましい。
PV2 - PV1の増減を Table 2.14 に示す。
ただし、d(PV2 - PV1)/dr = -25 / 3 / (1 + r)2
+ 28 / 3 / (1 + r)3 + 11 / (1 + r)4 (see below %o4)
d(PV2-PV1)/drの検算には、
Maxima, a Computer Algebra System
5.9.1 を用いた。
| r | 0 | (-11+√(1021))/25=0.838 | ∞ | ||
| d(PV2-PV1)/dr | 12 | + | 0 | - | 0 |
| PV2-PV1 | 0 | ↑ | 2.56 | ↓ | 0 |
PV2-PV1のグラフをFig. 2.14に示す。作図には、
gnuplot
version 4.0( Copyright (C) 1986 - 1993, 1998, 2004
Thomas Williams, Colin Kelley and many others)を用いた。
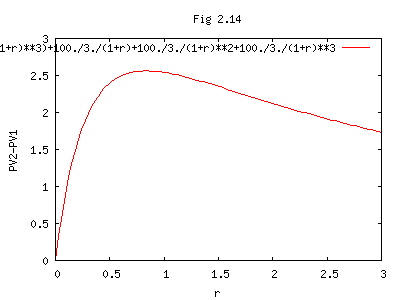
∴ 想定金利 r = 0.838 で後者と前者の減価償却の現在価値の差が最大となる。
図化コマンドを次のリンクに示す。(2011-10-26)
Maxima
Maximaで上を解く様子を次に示す。(added on 2016-11-03.)
Maxima 5.38.1 http://maxima.sourceforge.net
using Lisp SBCL 1.3.4
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) 25/(1+r)+38/(1+r)^2+37/(1+r)^3;
25 38 37
(%o1) ----- + -------- + --------
r + 1 2 3
(r + 1) (r + 1)
(%i2) 100/3/(1+r)+100/3/(1+r)^2+100/3/(1+r)^3;
100 100 100
(%o2) --------- + ---------- + ----------
3 (r + 1) 2 3
3 (r + 1) 3 (r + 1)
(%i3) %o2-%o1;
25 14 11
(%o3) --------- - ---------- - ----------
3 (r + 1) 2 3
3 (r + 1) 3 (r + 1)
(%i4) diff(%o3, r, 1);
25 28 11
(%o4) (- ----------) + ---------- + --------
2 3 4
3 (r + 1) 3 (r + 1) (r + 1)
(%i5) solve(%o4=0, r);
sqrt(1021) + 11 sqrt(1021) - 11
(%o5) [r = - ---------------, r = ---------------]
25 25
(%i6)
注
上のMaximaの出力は、「Commad line Maxima」の画面出力をコピーしたものである。
(ただし、OSは Windwos10 である。)
%i1他の入力行の最後の";"は、必要である。
%o1は、PV1 である。
%o2は、PV2 である。
%io3は、PV2-PV1 である。
%i4 は、%o3 を r で1回微分する。
%i5 は、%o4 = 0 を r について解く。
MathML
added on 2016-11-03.
MathMLの部分(italicの PV1, PV2, PV2 - PV1)は、 LibreOffice 5.2 の 「Math数式」 を用いた。
MathMLの作成方法
LibreOfficeの「Math数式」で数式を入力し、ファイルメニューの「名前を付けて保存」
で「ファイルの種類」を「MathML 2.0(.mml)(*.mml)」を選んで保存すると、
MathMLのファイルが作成される。ただし、Windows10の場合。
作成されたMathMLファイルから<math>タグで囲まれた部分をコピーして、
xhtmlファイルに貼り付けると、WEBブラウザに数式が綺麗に表示される。
For more information, see www.w3.org/Math/ .
history
2005-7-17、2005-7-24更新, revised on 2005-8-3, 2009-11-01, 2011-11-03, 2012-06-08, 2011-11-03,
2012-06-08.
2016-11-03 solution by Maxima added and mathematical expressions(PV1 and so on) in mathml added.
2021-02-11 change to html5, utf-8. add viewport.
2021-02-14 move history.