3.5

クーポン率 r = 0.1、額面価値 F(= 100 と仮定する。)、債権価格 P、満期利回り λ、1年当りのクーポン支払額 C = Fr、1年当りのクーポン支払回数 m = 1、 満期までの残りの利払期間 n = 20 - 5 = 15(年)とすると、 P と F は次式の関係を持ち、これを満たす λ が求める利回りである。
P > 1.05F、かつ、
P = F / (1 + (λ / m))ⁿ + (C / λ) (1 - 1 / (1 + (λ / m))ⁿ)

(f(λ) = P - 1.05 F を Fig. 3.5に示す。)

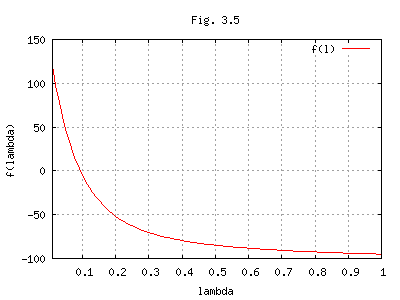
Frotran プログラムで λ を探すと、λ < 0.09366 = 9.366(%)

Python

code

# 3.5.py
# 18:21 2015-04-04

def g(x):
  return f/(1+x/m)**n+f*r/x*(1-1/(1+x/m)**n) -1.05*f

r = 0.1
f = 100
m = 1
n = 15
i = 1
eps = 1e-4
left = 0
right = 1
mid = (left + right) / 2

while abs(g(mid)) > eps:
  i = i + 1
  if(g(mid) > 0):
    left = mid
  else:
    right = mid
  mid = (left + right) / 2
lam = mid
print("labmda= ",round(lam,5))
print("{:}{:.6f}".format("f(lambda)=", g(lam)))
print("i=", i)
# end

output

labmda=  0.09366
f(lambda)=0.000056
i= 18

Fortran code

3.5.f90

GNUPLOT script file

図化コマンドを以下に示す。

# 3.5.plt
#
#
set terminal png small size 400,300 
set output '3.5.png'
set dummy l,y
set grid
set title "Fig. 3.5"
set xlabel "lambda"
set ylabel "f(lambda)"
f(l)=f/(1+(l/m))**n+(c/l)*(1-1/(1+(l/m))**n)-1.05*f
f = 100
m = 1
n = 15
c = 10.0
r = 0.1
plot [0.01:1] f(l)
# EOF 3.5.plt

history

2004-4-25. revised on 2004-05-01, 2007-05-03, 2011-10-29, 2011-11-03, 2014-08-15, 2015-04-04, 2016-10-10.
2011-10-29 画像ファイルをpngフォーマットに変更。
2011-11-03 awk file linked.
2014-08-15 awk changed to Fortran.
2015-04-04 python added.
2016-10-10 Fortran code linked. 2021-02-15 move history, change XHTML to html5, change shift-jis to utf-8, add viewport.