4.4
解法の説明
- 債券の額面(face value) F はすべて1000($)とする。
- 表4.6の1行目の債券を b0 と呼ぶ。他も同様。
- 最後の利払いからの経過日数
number_of_days_since_last_coupon
= (2011-11-5) - (2011-08-15)
= 82(days)
- 現在の利払い期間の日数
number_of_days_in_current_coupon_perod
= (2012-2-15) - (2011-08-15)
= 184(days)
- 債券 b0 の価格
= 額面* 売値
= (face value) * (ask price)
= 1000 * 100.00(%)
= 1000($)
- 債券 b0 のクーポン額
coupon amount
= C/m = 額面 * クーポン率 / 2
= (face value) * (coupon rate) / 2
= 1000 * 6.625 / 100 / 2
= 33.13($)
ただし、mは1年あたりのクーポン支払回数(the number of coupon payments per year) - 債券 b0 の経過利息, accrued interest, AI
AI = 最後の利払いからの経過日数 / 現在の利払い期間の日数 * クーポン額
= 82 / 184 * 33.13 = 14.76($)
- 債券 b0 の総価格,
total price
= 価格 + 経過利息(AI)
= 1000 + 14.76
= 1014.76($)
債券のキャッシュフロー流列(cash flow stream), cfi は、次の通りとなる。 ただし、小数点以下は、見易さを優先するために、切り捨てで表示する。
cf0 = (-1014, 33+1000) cf1 = (-1027, 45+1000) cf2 = (-1025, 39, 39+1000) cf3 = (-1028, 41, 41+1000) cf4 = (-1030, 41, 41, 41+1000) cf5 = (-1032, 41, 41, 41+1000) cf6 = (-1025, 40, 40, 40, 40+1000) cf7 = (-1039, 43, 43, 43, 43+1000) cf8 = ( -996, 34, 34, 34, 34, 34+1000) cf9 = (-1042, 44, 44, 44, 44, 44+1000) cf10 = ( -989, 34, 34, 34, 34, 34, 34+1000) cf11 = (-1036, 43, 43, 43, 43, 43, 43+1000) cf12 = (-1008, 38, 38, 38, 38, 38, 38, 38+1000) cf13 = (-1116, 56, 56, 56, 56, 56, 56, 56+1000) cf14 = (-1033, 42, 42, 42, 42, 42, 42, 42, 42+1000) cf15 = (-1101, 52, 42, 42, 42, 42, 42, 42, 42+1000) cf16 = (-1011, 39, 39, 39, 39, 39, 39, 39, 39, 39+1000) cf17 = (-1049, 44, 44, 44, 44, 44, 44, 44, 44, 44+1000)
上のキャッシュフローを、
総価格 = 各クーポンの現在価値 + 満期時入金の現在価値
の等式に書き換えて、次の各式を得る。ただし、d(ti)は割引係数である。
1014 = 1033d(t0) 1027 = 1045d(t0) 1025 = 39d(t0)+1039d(t1) 1028 = 41d(t0)+1041d(t1) 1030 = 41d(t0)+ 41d(t1)+1041d(t2) 1032 = 41d(t0)+ 41d(t1)+1041d(t2) 1025 = 40d(t0)+ 40d(t1)+ 40d(t2)+1040d(t3) 1039 = 43d(t0)+ 43d(t1)+ 43d(t2)+1043d(t3) 996 = 34d(t0)+ 34d(t1)+ 34d(t2)+ 34d(t3)+1034d(t4) 1024 = 44d(t0)+ 44d(t1)+ 44d(t2)+ 44d(t3)+1044d(t4) 989 = 34d(t0)+ 34d(t1)+ 34d(t2)+ 34d(t3)+ 34d(t4)+1034d(t5) 1036 = 43d(t0)+ 43d(t1)+ 43d(t2)+ 43d(t3)+ 43d(t4)+1043d(t5) 1008 = 38d(t0)+ 38d(t1)+ 38d(t2)+ 38d(t3)+ 38d(t4)+ 38d(t5)+1038d(t6) 1116 = 56d(t0)+ 56d(t1)+ 56d(t2)+ 56d(t3)+ 56d(t4)+ 56d(t5)+1056d(t6) 1033 = 42d(t0)+ 42d(t1)+ 42d(t2)+ 42d(t3)+ 42d(t4)+ 42d(t5)+ 42d(t6)+1042d(t7) 1101 = 52d(t0)+ 52d(t1)+ 52d(t2)+ 52d(t3)+ 52d(t4)+ 52d(t5)+ 52d(t6)+1052d(t7) 1011 = 39d(t0)+ 39d(t1)+ 39d(t2)+ 39d(t3)+ 39d(t4)+ 39d(t5)+ 39d(t6)+ 39d(t7)+1039d(t8) 1049 = 44d(t0)+ 44d(t1)+ 44d(t2)+ 44d(t3)+ 44d(t4)+ 44d(t5)+ 44d(t6)+ 44d(t7)+1044d(t8)
上の式を、次の形式で表現する。
{y} = [W]{β}
ただし、{y}は、(1014 1027 ... 1049)の転置ベクトル、{β}は、
(d(t0) d(t1) ... d(t8))の転置ベクトル、
そして、行列[W]は、 ┌ ┐ │1033 0 0 0 0 0 0 0 0│ │1045 0 0 0 0 0 0 0 0│ │ 39 1039 0 0 0 0 0 0 0│ │ 41 1041 0 0 0 0 0 0 0│ │ 41 41 1041 0 0 0 0 0 0│ │ 41 41 1041 0 0 0 0 0 0│ │ 40 40 40 1041 0 0 0 0 0│ │ 43 43 43 1043 0 0 0 0 0│ │ 34 34 34 34 1034 0 0 0 0│ │ 44 44 44 44 1044 0 0 0 0│ │ 34 34 34 34 34 1034 0 0 0│ │ 43 43 43 43 43 1043 0 0 0│ │ 38 38 38 38 38 38 1038 0 0│ │ 56 56 56 56 56 56 1056 0 0│ │ 42 42 42 42 42 42 42 1042 0│ │ 52 52 52 52 52 52 52 1052 0│ │ 39 39 39 39 39 39 39 39 1039│ │ 44 44 44 44 44 44 44 44 1044│ └ ┘ である。
上の {y}=[W]{β}の{β}をPythonのnumpyのlinalg.lstsq(最小二乗法)で求め、 その結果βi=d(ti)とtiを下表に示す。
| i | ti(year) | βi =d(ti) |
| 0 | 0.279 | 0.982 |
| 1 | 0.778 | 0.949 |
| 2 | 1.282 | 0.913 |
| 3 | 1.778 | 0.877 |
| 4 | 2.282 | 0.840 |
| 5 | 2.778 | 0.804 |
| 6 | 3.282 | 0.771 |
| 7 | 3.778 | 0.740 |
| 8 | 4.282 | 0.712 |
d(t)=e-r(t)tから、r(t)は次式となる。
r(t)=-log(d(t))/t
tiと上式から求めたr(ti)を下表に示す。
| i | ti(year) | r(ti) |
| 0 | 0.279 | 0.0638 |
| 1 | 0.778 | 0.0672 |
| 2 | 1.282 | 0.0707 |
| 3 | 1.778 | 0.0737 |
| 4 | 2.282 | 0.0763 |
| 5 | 2.778 | 0.0781 |
| 6 | 3.282 | 0.0792 |
| 7 | 3.778 | 0.0794 |
| 8 | 4.282 | 0.0790 |
上表のtiとriから、 次の多項式の係数を最小二乗法で求める。
r(t) = a0 + a1t + a2t2 + a3t3 + a4t4
r(t)の多項式の係数を求めるにあたり、 tiとr(ti)の関係を次式で表し、 r(t)の多項式の係数を最小二乗法で推定する。
{y2} = [W2]{β2}
ただし、
{y2}=
| • |
| ri(ti) |
| • |
=
| 0.0638 |
| 0.0672 |
| 0.0707 |
| 0.0737 |
| 0.0763 |
| 0.0781 |
| 0.0792 |
| 0.0794 |
| 0.0790 |
[W2]=
| • | • | • | • | • |
| 1 | ti | ti2 | ti3 | ti4 |
| • | • | • | • | • |
=
| 1.000 | 0.279 | 0.078 | 0.022 | 0.006 |
| 1.000 | 0.778 | 0.605 | 0.471 | 0.367 |
| 1.000 | 1.282 | 1.644 | 2.108 | 2.703 |
| 1.000 | 1.778 | 3.162 | 5.622 | 9.996 |
| 1.000 | 2.282 | 5.208 | 11.887 | 27.127 |
| 1.000 | 2.778 | 7.718 | 21.441 | 59.564 |
| 1.000 | 3.282 | 10.773 | 35.358 | 116.053 |
| 1.000 | 3.778 | 14.274 | 53.928 | 203.744 |
| 1.000 | 4.282 | 18.337 | 78.523 | 336.252 |
{β2}=
| a0 |
| a1 |
| a2 |
| a3 |
| a4 |
∴estimated{β2} =
| 0.0621 |
| 0.00607 |
| 0.00125 |
| -0.000638 |
| 0.0000540 |
(注 βの最小二乗推定には、 Python の numpyのlinalg.lstsq(最小二乗法)を用いた。)
よって期間構造の推定式は、次式となる。
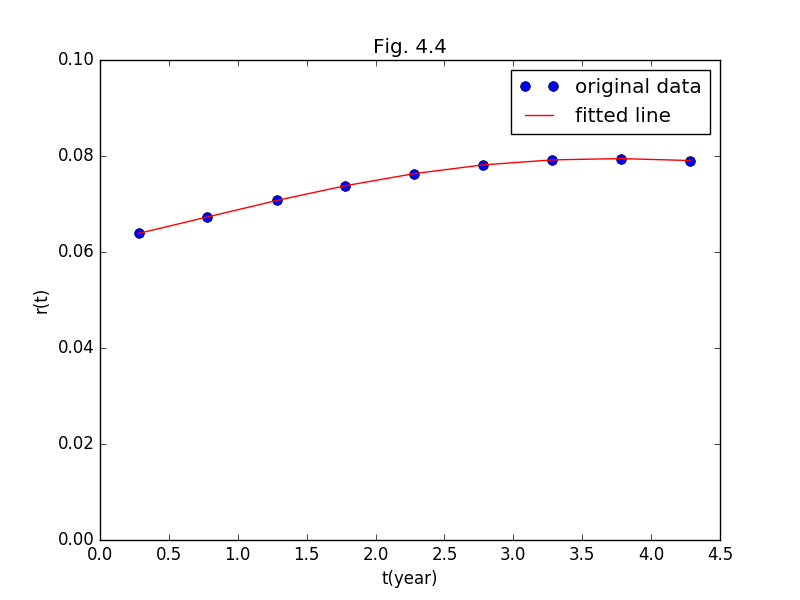
r(t) = 0.0621 + 0.00607t + 0.00125t2 - 0.000638t3
+ 0.0000540t4
期間構造カーブとその基データをFig.4.4に示す。
解法の解説1
1)
債券のキャッシュフローから債券の現在価値の方程式
Pi = Σci(tj) d(tj)
ただし、
Piは債権iの総価格、
ci(tj)は債券iの時点tjのキャッシュフロー、
d(tj)は時点tjに対する割引係数である。
を作成する。
この方程式を各債券に対して作成し、連立方程式にする。
P0 = c0(t0)d(t0) + … + c0(t8)d(t8) .
.
..
.
..
.
.P17 = c17(t0)d(t0) + … + c17(t8)d(t8)
上を行列表示にすると、次が得られる。
{y} = [W]{β}
ただし、
- {y}は、債券の総価格P0, ..., P17 を要素とする縦ベクトルである。{y}は、既知である。
- [W]は、債券iのd(tj)の係数ci(tj) を横に並べたものをi=0からi=17の順に縦に積み重ねた行列である。 ただし、ci(tj)は、 t = tjにおける債券iのキャッシュフローである。 [W]は、既知である。
- {β}は、d(t0), ..., d(t8) を要素とする縦ベクトルである。{β}は、未知である。
この連立方程式は、未知数が9個で、方程式が18個である。 未知数に対して方程式が多いので、方程式の解は求まらない。 そこで、最小二乗推定で未知数 d(t0), ..., d(t8)を推定する。
numpyのlinalg.lstsqを{y}と[W]に適用すると、{β}の最小二乗推定値が求まる。 すなわち、d(t0)からd(t8)の最小二乗推定値が求まる。
2)
d(t0), ..., d(t8)から連続複利のスポットレート
r(t0), ...,
r(t8)を求める。
3)
r(t)を、
r(t) = a0 + a1t + a2t2
+ a3t3 + a4t4
の形で推定するので、次の連立方程式を作成する。
r(t0) = a0 + a1t0 + a2t02 + a3t03 + a4t04
r(t1) = a0 + a1t1 + a2t12 + a3t13 + a4t14
r(t2) = a0 + a1t2 + a2t22 + a3t23 + a4t24
r(t3) = a0 + a1t3 + a2t32 + a3t33 + a4t34
r(t4) = a0 + a1t4 + a2t42 + a3t43 + a4t44
r(t5) = a0 + a1t5 + a2t52 + a3t53 + a4t54
r(t6) = a0 + a1t6 + a2t62 + a3t63 + a4t64
r(t7) = a0 + a1t7 + a2t72 + a3t73 + a4t74
r(t8) = a0 + a1t8 + a2t82 + a3t83 + a4t84
この連立方程式は、未知数aiが5個、方程式が9個である。 未知数の数より方程式の数が多いため、未知数は求まらない。 そこで、未知数aiを最小二乗推定する。 上の連立方程式を次の行列表示にする。
{r(ti)}
=[1 ti ti2 ti3 ti4 in i-th row]
{ai}
この連立方程式の
{r}は既知、行列[]は既知、{ai}は未知である。
{r}と行列[]とから最小二乗推定により{ai}を求める。
解法の解説2
-
総価格{Pi}とキャッシュフロー[ci(tj)]
とから割引係数{d(ti)}の最小二乗推定値を得る。
ただし、 {Pi}=[ci(tj)]{d(tj)}、 iは行を、jは列を表す。(i=0,...,17; j=0,...,8)
{}は列ベクトルを、[ ]は行列を表す。 - {d(ti)}から、連続複利のスポットレート{r(ti)}を求める。 (i=0,...,8)
-
r(t)を次の形で推定するために、
r(t) = a0 + a1t1 + a2t2 + a3t3 + a4t4
{r(ti)} = [Wij]{aj}となる[W]を次の通り作成する。 (i=0,...,8; j=0,...,4)
[Wi] = [1 ti ti2 ti3 ti4 in i-th row]
{r(ti)}と[Wij]とから最小二乗推定値{aj}を得る。
解法の解説3
- 債券の総価格(ask price and AI)と、クーポンC/m及び額面Fの現在価値とから、 割引係数d(ti)を最小二乗推定する。
- 割引係数d(ti)から、 連続複利のスポットレートr(ti)を算定する。
- 離散データ(ti, r(ti))から連続値である r(t) = a0 + a1t1 + a2t2 + a3t3 + a4t4 の t の係数 aj を最小二乗推定する。
解法の実装 in Python 3
code
解法を実装したPython 3 のcode を次に示す。
# 4.4.numpy.py # created on 2016-11-26 # # import datetime import math import numpy as np import matplotlib.pyplot as plt from pylab import axis, title, xlabel, ylabel date = datetime.date log = math.log # input face_value = 1000 coupon_rate = np.array([6 + 5/8, 9 + 1/8, 7 + 7/8, 8 + 1/4, 8 + 1/4, \ 8 + 3/8, 8, 8 + 3/4, 6 + 7/8, 8 + 7/8, \ 6 + 7/8, 8 + 5/8, 7 + 3/4, 11 + 1/4, 8 + 1/2, \ 10 + 1/2, 7 + 7/8, 8 + 7/8]) maturity = np.array([[2012, 2], [2012, 2], [2012, 8], [2012, 8], \ [2013, 2], [2013, 2], [2013, 8], [2013, 8], \ [2014, 2], [2014, 2], [2014, 8], [2014, 8], \ [2015, 2], [2015, 2], [2015, 8], [2015, 8], \ [2016, 2], [2016, 2]]) ask_price = np.array([100+ 0/32, 100+22/32, 100+24/32, 101+1/32, 101+ 7/32, \ 101+12/32, 100+26/32, 102+ 1/32, 98+5/32, 102+ 9/32, \ 97+13/32, 101+23/32, 99+ 5/32, 109+4/32, 101+13/32, \ 107+27/32, 99+13/32, 103+ 0/32]) today = date(2011, 11, 5) last_coupon = date(2011, 8, 15) next_coupon = date(2012, 2, 15) # calculate coupon = face_value * coupon_rate / 100 / 2 t = np.array([(date(2012, 2, 15) - today).days / 365, \ (date(2012, 8, 15) - today).days / 365, \ (date(2013, 2, 15) - today).days / 365, \ (date(2013, 8, 15) - today).days / 365, \ (date(2014, 2, 15) - today).days / 365, \ (date(2014, 8, 15) - today).days / 365, \ (date(2015, 2, 15) - today).days / 365, \ (date(2015, 8, 15) - today).days / 365, \ (date(2016, 2, 15) - today).days / 365]) number_of_days_since_last_coupon = (today - last_coupon).days number_of_days_in_current_coupon_period = (next_coupon - last_coupon).days accrued_interest = number_of_days_since_last_coupon \ / number_of_days_in_current_coupon_period \ * coupon total_price = face_value * ask_price / 100 + accrued_interest cf0 =np.array([coupon[ 0]+face_value,0,0,0,0,0,0,0,0]) cf1 =np.array([coupon[ 1]+face_value,0,0,0,0,0,0,0,0]) cf2 =np.array([coupon[ 2],coupon[ 2]+face_value,0,0,0,0,0,0,0]) cf3 =np.array([coupon[ 3],coupon[ 3]+face_value,0,0,0,0,0,0,0]) cf4 =np.array([coupon[ 4],coupon[ 4],coupon[ 4]+face_value,0,0,0,0,0,0]) cf5 =np.array([coupon[ 5],coupon[ 5],coupon[ 5]+face_value,0,0,0,0,0,0]) cf6 =np.array([coupon[ 6],coupon[ 6],coupon[ 6],coupon[ 6]+face_value, \ 0,0,0,0,0]) cf7 =np.array([coupon[ 7],coupon[ 7],coupon[ 7],coupon[ 7]+face_value, \ 0,0,0,0,0]) cf8 =np.array([coupon[ 8],coupon[ 8],coupon[ 8],coupon[ 8],coupon[ 8]+ \ face_value,0,0,0,0]) cf9 =np.array([coupon[ 9],coupon[ 9],coupon[ 9],coupon[ 9],coupon[ 9]+ \ face_value,0,0,0,0]) cf10=np.array([coupon[10],coupon[10],coupon[10],coupon[10],coupon[10], \ coupon[10]+face_value,0,0,0]) cf11=np.array([coupon[11],coupon[11],coupon[11],coupon[11],coupon[11], \ coupon[11]+face_value,0,0,0]) cf12=np.array([coupon[12],coupon[12],coupon[12],coupon[12],coupon[12], \ coupon[12],coupon[12]+face_value,0,0]) cf13=np.array([coupon[13],coupon[13],coupon[13],coupon[13],coupon[13], \ coupon[13],coupon[13]+face_value,0,0]) cf14=np.array([coupon[14],coupon[14],coupon[14],coupon[14],coupon[14], \ coupon[14],coupon[14],coupon[14]+face_value,0]) cf15=np.array([coupon[15],coupon[15],coupon[15],coupon[15],coupon[15], \ coupon[15],coupon[15],coupon[15]+face_value,0]) cf16=np.array([coupon[16],coupon[16],coupon[16],coupon[16],coupon[16], \ coupon[16],coupon[16],coupon[16],coupon[16]+face_value]) cf17=np.array([coupon[17],coupon[17],coupon[17],coupon[17],coupon[17], \ coupon[17],coupon[17],coupon[17],coupon[17]+face_value]) w1 = np.vstack((cf0, cf1, cf2, cf3, cf4, cf5, cf6, cf7, cf8, cf9, \ cf10,cf11,cf12,cf13,cf14,cf15,cf16,cf17)) y1 = total_price p1 = np.linalg.lstsq(w1, y1) beta1 = p1[0] r = list(map(lambda x, y: - log(x) / y, beta1, t)) w2 = np.vstack([np.ones(len(t)), t, t ** 2, t ** 3, t ** 4]).T y2 = r p2 = np.linalg.lstsq(w2, y2) beta2 = p2[0] # output print('4.4.numpy.py') print('{:15}{}'.format('face value', face_value)) print('{:15}{}'.format('last_coupon', last_coupon)) print('{:15}{}'.format('today', today )) print('{:15}{}'.format('next coupon', next_coupon)) print('number_of_days_since_last_coupon= ', \ number_of_days_since_last_coupon) print('number_of_days_in_current_coupon_period= ', \ number_of_days_in_current_coupon_period) print() fmt1='{:>15}{:>15}{:>15}{:>15}{:>15}' fmt2='{:15}{:15.2f}{:15.2f}{:15.2f}{:15.2f}' print(fmt1.format('i', 'ask price','coupon amount','a. interest','total price')) print(75 * '-') for i in range(len(ask_price)): print(fmt2.format(i, ask_price[i], coupon[i], accrued_interest[i], \ total_price[i])) print(75 * '-') print() print('{:>7}'.format('i'), end='') for i in range(len(t)): print('{:7}'.format(i), end='') print() print(70 * '-') print('{:>7}'.format('t[i]'), end='') for i in range(len(t)): print('{:7.3f}'.format(t[i]), end='') print() print(70 * '-') print() print('y1, total price') print('{:>10}{:>10}'.format('i', 'y1[i]')) print(20 * '-') for i in range(len(y1)): print('{:10}{:10d}'.format(i, int(y1[i]))) print(20 * '-') print() print('w1, matrix of cf(in integer) in row') print('{:>7}'.format('i') , end='') for i in range(len(t)): print('{:>6}{:1}'.format('t', i), end='') print() print(70 * '-') for i in range(len(w1)): print('{:7}'.format(i), end='') for j in range(len(w1[0])): print('{:7}'.format(int(w1[i][j])), end='') print() print(70 * '-') print() print('estimated beta1, d(t[i])') print('{:>10}{:>10}'.format('i', 'beta1[i]')) print(20*'-') for i in range(len(beta1)): print('{:10}{:10.3f}'.format(i, beta1[i])) print(20 * '-') print() print('estimated r(t[i])') print('{:>10}{:>10}'.format('i','r(t[i])')) print(20 * '-') for i in range(len(r)): print('{:10}{:10.4f}'.format(i, r[i])) print(20 * '-') print() print('w2, coefficent matrix') fmt3='{:>10}{:>10}{:>10}{:>10}{:>10}{:>10}' print(fmt3.format('i', 1, 't', 't^2', 't^3', 't^4')) print(60 * '-') for i in range(len(w2)): print('{:10}'.format(i), end='') for j in range(len(w2[0])): print('{:10.3f}'.format(w2[i][j]), end='') print() print(60 * '-') print() print('beta2, estimated a[i] for r(t)') print('{:>10}{:5}{:}'.format('i', '', 'a[i]')) print(40 * '-') for i in range(len(beta2)): print('{:10}{:5}{:}'.format(i, ' ', beta2[i])) print(40 * '-') print() a = beta2 print() print('estimated r(t)=', \ a[0], '+', a[1], 't +', a[2], 't^2 +', a[3], 't^3 +', a[4], 't^4') # plot def f(t): return sum([a[i] * t ** i for i in range(len(a))]) x = t y = r axis(ymin = 0) axis(ymax = 0.1) title('Fig. 4.4') xlabel('t(year)') ylabel('r(t)') plt.plot(x, y, 'o', label = 'original data', markersize = 7) plt.plot(x, f(x), 'r', label = 'fitted line') plt.legend() plt.show()
output
codeの出力を次に示す。
4.4.numpy.py
face value 1000
last_coupon 2011-08-15
today 2011-11-05
next coupon 2012-02-15
number_of_days_since_last_coupon= 82
number_of_days_in_current_coupon_period= 184
i ask price coupon amount a. interest total price
---------------------------------------------------------------------------
0 100.00 33.12 14.76 1014.76
1 100.69 45.62 20.33 1027.21
2 100.75 39.38 17.55 1025.05
3 101.03 41.25 18.38 1028.70
4 101.22 41.25 18.38 1030.57
5 101.38 41.88 18.66 1032.41
6 100.81 40.00 17.83 1025.95
7 102.03 43.75 19.50 1039.81
8 98.16 34.38 15.32 996.88
9 102.28 44.38 19.78 1042.59
10 97.41 34.38 15.32 989.38
11 101.72 43.12 19.22 1036.41
12 99.16 38.75 17.27 1008.83
13 109.12 56.25 25.07 1116.32
14 101.41 42.50 18.94 1033.00
15 107.84 52.50 23.40 1101.83
16 99.41 39.38 17.55 1011.61
17 103.00 44.38 19.78 1049.78
---------------------------------------------------------------------------
i 0 1 2 3 4 5 6 7 8
----------------------------------------------------------------------
t[i] 0.279 0.778 1.282 1.778 2.282 2.778 3.282 3.778 4.282
----------------------------------------------------------------------
y1, total price
i y1[i]
--------------------
0 1014
1 1027
2 1025
3 1028
4 1030
5 1032
6 1025
7 1039
8 996
9 1042
10 989
11 1036
12 1008
13 1116
14 1033
15 1101
16 1011
17 1049
--------------------
w1, matrix of cf(in integer) in row
i t0 t1 t2 t3 t4 t5 t6 t7 t8
----------------------------------------------------------------------
0 1033 0 0 0 0 0 0 0 0
1 1045 0 0 0 0 0 0 0 0
2 39 1039 0 0 0 0 0 0 0
3 41 1041 0 0 0 0 0 0 0
4 41 41 1041 0 0 0 0 0 0
5 41 41 1041 0 0 0 0 0 0
6 40 40 40 1040 0 0 0 0 0
7 43 43 43 1043 0 0 0 0 0
8 34 34 34 34 1034 0 0 0 0
9 44 44 44 44 1044 0 0 0 0
10 34 34 34 34 34 1034 0 0 0
11 43 43 43 43 43 1043 0 0 0
12 38 38 38 38 38 38 1038 0 0
13 56 56 56 56 56 56 1056 0 0
14 42 42 42 42 42 42 42 1042 0
15 52 52 52 52 52 52 52 1052 0
16 39 39 39 39 39 39 39 39 1039
17 44 44 44 44 44 44 44 44 1044
----------------------------------------------------------------------
estimated beta1, d(t[i])
i beta1[i]
--------------------
0 0.982
1 0.949
2 0.913
3 0.877
4 0.840
5 0.805
6 0.771
7 0.741
8 0.713
--------------------
estimated r(t[i])
i r(t[i])
--------------------
0 0.0639
1 0.0673
2 0.0708
3 0.0738
4 0.0763
5 0.0781
6 0.0792
7 0.0794
8 0.0791
--------------------
w2, coefficent matrix
i 1 t t^2 t^3 t^4
------------------------------------------------------------
0 1.000 0.279 0.078 0.022 0.006
1 1.000 0.778 0.605 0.471 0.367
2 1.000 1.282 1.644 2.108 2.703
3 1.000 1.778 3.162 5.622 9.996
4 1.000 2.282 5.208 11.887 27.127
5 1.000 2.778 7.718 21.441 59.564
6 1.000 3.282 10.773 35.358 116.053
7 1.000 3.778 14.274 53.928 203.744
8 1.000 4.282 18.337 78.523 336.252
------------------------------------------------------------
beta2, estimated a[i] for r(t)
i a[i]
----------------------------------------
0 0.062086370760156565
1 0.006071621745898055
2 0.0012515798717840998
3 -0.0006384168097172578
4 5.398054834520206e-05
----------------------------------------
estimated r(t)= 0.0620863707602 + 0.0060716217459 t + 0.00125157987178 t^2 + -0.000638416809717 t^3 + 5.39805483452e-05 t^4
既に上に示した図は、Python の codeによりプロットした図である。
JavaScript code
2024-11-02 4.4.js for node.js
Gauche code
2024-11-02 4.4.scm
Julia code
2024-11-02 4.4.jl (2024-12-07 revise, 2025-02-01 open.)
Fortran code
2024-11-02 4.4.f90 (2024-12-07 revise, 2025-02-01 open.)
history
2004-09-24 create.
2011-11-02 revised.
2016-04-04 estimation of β in Gauche added.
2016-04-09 estimations of β in gnupot and Python added.
2016-10-15 Gauche code linked.
2016-11-05 estimation of β in Maxima added.
2016-11-20 estimation of β by numpy.linalg.lstsq added.
2016-11-26 all revised for correcting d(t) function.
2021-02-17 change XHTML to html5, change shift-jis to utf-8, add viewport.
2024-11-02 add a JavaScript code, a Gauche code, a Julia code and a Fortran code.
2025-02-01 open revised 4.4.jl, revised 4.4.f90.