6.3

2005-2-23, revised on 2011-08-28, 2011-10-26, 2011-11-03, 2012-06-08.
2016-11-05 solution of α with Maxima added.

条件
資産Aと資産Bの相関係数 ρ = 0.1 (1)
平均r_A = 0.100 (2)
平均r_B = 0.180 (3)
σ_A = 0.15 (4)
σ_B = 0.30 (5)

(a)

AとBを組合わせたポートフォリオの分散は、次式となる。

σ² = Σw_iw_jσ_ij (i,j = 1,2) (6)
ただし、
w₁ = α (7)
w₂ = 1 - α (8)
σ₁₁ = σ_A² (9)
σ₁₂ = σ_AB (10)
σ₂₁ = σ_AB (11)
σ₂₂ = σ_B² (12)
σ_AB = ρσ_Aσ_B (13)

式(6)に式(1), (4),(5),(7)～(13)を代入すると、次式となる。
σ² = w₁w₁σ₁₁ + w₁w₂σ₁₂ + w₂w₁σ₂₁ + w₂w₂σ₂₂₂)
= αασ_A² + α(1 - α)σ_AB + (1 - α)ασ_AB + (1 - α)(1 - α)σ_B²
= 0.0225 α² + 0.0045α(1 - α) + 0.0045α(1 - α) + (0.09 - 0.18 α + 0.09 α²)
= 0.1035 α² - 0.171 α + 0.09
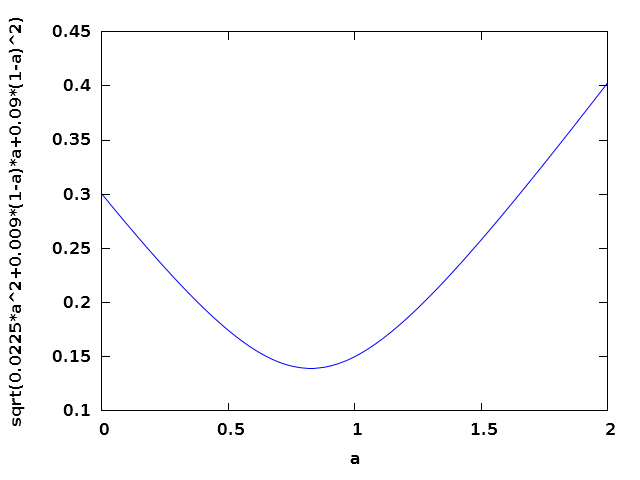
∴ 標準偏差σ = √(0.1035 α² - 0.171 α + 0.09) (14)

式(14)のグラフをFig.6.3.1に示す。
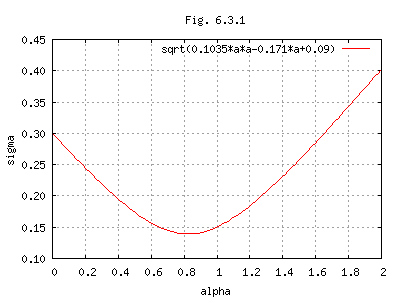
graph

式(14)を α で微分すると、次式となる。
d(σ)/dα = (1/2)(0.1035 α² - 0.171 α + 0.09)^-(1/2)(0.207 α - 0.171) (15)

式(15)のグラフをFig.6.3.2に示す。
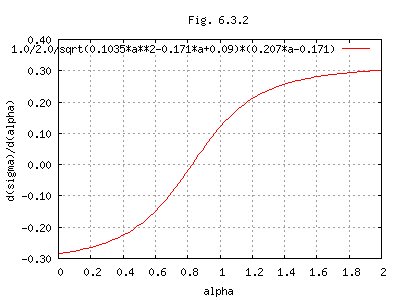
graph

以上によりd(σ)/dα = 0 を満たす α のとき、σは最小値となる。

よって、α と 1 - α は、次となる。
∴ α = 0.171 / 0.207 = 0.826 (16)
∴ 1 - α = 1 - 0.826 = 0.174

(b)

最小標準偏差の値 σ_min は、式(14)に式(16)を代入して求める。
∴σ_min = σ(0.826) = 0.139

(c)

このポートフォリオの期待収益率E(r)は、次式となる。
E(r) = α平均r_A + (1 - α)平均r_B (17)
= 0.826 * 0.100 + 0.174 * 0.180 = 0.114
∴ E(r) = 11.4%

Maxima による α の解法

2016-11-05
Maxima による α の解法とMaximaで作成した図を次に示す。

解は、手計算と一致した。

注
%i1 to %i12 与条件の入力
%i13 σ² の作成
%i14 σ の作成
%i15 σ を変数a で微分する
%i16 σ の導関数=0 を a に対して解き、解を返す
%i17 解a を小数で表示
%i18 定義域を[0, 1]とするσ のグラフを png形式でファイル出力する


Maxima 5.38.1 http://maxima.sourceforge.net
using Lisp SBCL 1.3.4
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) rho : 0.1;
(%o1)                                 0.1
(%i2) ra  : 0.1;
(%o2)                                 0.1
(%i3) rb  : 0.18;
(%o3)                                0.18
(%i4) sa  : 0.15;
(%o4)                                0.15
(%i5) sb  : 0.3;
(%o5)                                 0.3
(%i6) sab : rho * sa * sb;
(%o6)                               0.0045
(%i7) w1  : a;
(%o7)                                  a
(%i8) w2  : 1 - a;
(%o8)                                1 - a
(%i9) s11 : sa ^ 2;
(%o9)                               0.0225
(%i10) s12 : sab;
(%o10)                              0.0045
(%i11) s21 : sab;
(%o11)                              0.0045
(%i12) s22 : sb ^ 2;
(%o12)                               0.09
(%i13) w1*w1*s11 + w1*w2*s12 + w2*w1*s21 + w2*w2*s22;
                          2                                 2
(%o13)            0.0225 a  + 0.009 (1 - a) a + 0.09 (1 - a)
(%i14) sigma : sqrt(%);
                            2                                 2
(%o14)         sqrt(0.0225 a  + 0.009 (1 - a) a + 0.09 (1 - a) )
(%i15) diff(sigma, a, 1);
                            0.036 a - 0.171 (1 - a)
(%o15)        ---------------------------------------------------
                             2                                 2
              2 sqrt(0.0225 a  + 0.009 (1 - a) a + 0.09 (1 - a) )
(%i16) solve(%, a);

rat: replaced -0.171 by -171/1000 = -0.171

rat: replaced 0.036 by 9/250 = 0.036

rat: replaced 0.09 by 9/100 = 0.09

rat: replaced 0.009 by 9/1000 = 0.009

rat: replaced 0.0225 by 9/400 = 0.0225
                                        19
(%o16)                             [a = --]
                                        23
(%i17) float(%);
(%o17)                     [a = 0.8260869565217391]
(%i18) plot2d(sigma, [a, 0, 2], [png_file, "6.3.mac.png"]);
(%o18)      [C:/Users/***/maxout780.gnuplot, C:/Users/***/6.3.mac.png]
(%i19)

備考

式(14)、(17)から得られる平均―標準偏差ダイヤグラムをFig.6.3.3に示す。
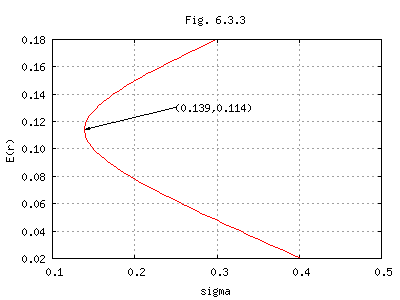
graph

図化コマンド

図化コマンドを次のリンクに示す。

history

2005-2-23, revised on 2011-08-28, 2011-10-26, 2011-11-03, 2012-06-08.
2016-11-05 solution of α with Maxima added.
2021-02-17 change XHTML to html5, change shift-jis to utf-8, add viewport.