6.5

(created on 2004-8-8, revised on 2005-2-16, 2011-10-26, 2011-10-29, 2011-11-03.)
2011-10-29 画像ファイルをpngフォーマットに変更した。
2011-11-03 Table 6.5 added.
2016-11-06 (a),(b) revised and solution with Maxima added.

Maxima calculation

Maximaによる解を示す。

期待収益 E(R) の式を、%o5 に得。
分散 var(R) の最小値を、%o10 に得。
分散の最小値に対応する期待収益率 E(r) の値を、%o12 に得。

注
%i1 雨が降らない場合の総収益を x1 に代入
%i2 雨が降る場合の総収益を x2 に代入
%i3 雨が降らない確率を p1 に代入
%i4 雨が降る確率を p2 に代入
%i5 総収益 x の期待値 E(x) を Ex に代入
%i6 期待値 E(x²) を Exx に代入
%i7 総収益 x の分散 var(x) = E(x²) - E(x)² を、変数 variance に代入
%i8 分散 variance を u で微分して得た導関数を、変数 derivative に代入
%i9 導関数 derivative を 0 とする u を求め、解 u=3000000 を Au に代入
%i10 解 u を variance に代入し、分散の最小値 0.0 を得
%i11 解 u を Ex に代入し、分散が最小の場合の期待総収益の値 1.2 を得
%i12 期待総収益 = 1.2 から、期待収益率E(r) = 1.2 - 1.0 = 0.2 = 20% を得


Maxima 5.38.1 http://maxima.sourceforge.net
using Lisp SBCL 1.3.4
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) x1 : 3e6 / (1e6 + 0.5 * u);
                                   3000000.0
(%o1)                          -----------------
                               0.5 u + 1000000.0
(%i2) x2 : u   / (1e6 + 0.5 * u);
                                       u
(%o2)                          -----------------
                               0.5 u + 1000000.0
(%i3) p1 : 0.5;
(%o3)                                 0.5
(%i4) p2 : 0.5;
(%o4)                                 0.5
(%i5) Ex : x1 * p1 + x2 * p2;
                           0.5 u             1500000.0
(%o5)                ----------------- + -----------------
                     0.5 u + 1000000.0   0.5 u + 1000000.0
(%i6) Exx : x1^2 * p1 + x2^2 * p2;
                              2
                         0.5 u                 4.5e+12
(%o6)             -------------------- + --------------------
                                     2                      2
                  (0.5 u + 1000000.0)    (0.5 u + 1000000.0)
(%i7) variance : Exx - Ex^2;
                                                                 2
                0.5 u             1500000.0     2           0.5 u
(%o7) (- (----------------- + -----------------) ) + --------------------
          0.5 u + 1000000.0   0.5 u + 1000000.0                         2
                                                     (0.5 u + 1000000.0)
                                                                 4.5e+12
                                                         + --------------------
                                                                              2
                                                           (0.5 u + 1000000.0)
(%i8) derivative : diff(variance, u);
                     2
                0.5 u                         0.25 u
(%o8) (- --------------------) - 2 ((- --------------------)
                            3                             2
         (0.5 u + 1000000.0)           (0.5 u + 1000000.0)
          0.5                750000.0
 + ----------------- - --------------------)
   0.5 u + 1000000.0                      2
                       (0.5 u + 1000000.0)
        0.5 u             1500000.0               1.0 u
 (----------------- + -----------------) + --------------------
  0.5 u + 1000000.0   0.5 u + 1000000.0                       2
                                           (0.5 u + 1000000.0)
         4.5e+12
 - --------------------
                      3
   (0.5 u + 1000000.0)
(%i9) Au : solve(derivative, u);

rat: replaced -4.5e+12 by -4500000000000/1 = -4.5e+12
rat: replaced 1000000.0 by 1000000/1 = 1000000.0
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced 1.0 by 1/1 = 1.0
rat: replaced 1000000.0 by 1000000/1 = 1000000.0
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced -750000.0 by -750000/1 = -750000.0
rat: replaced 1000000.0 by 1000000/1 = 1000000.0
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced 1000000.0 by 1000000/1 = 1000000.0
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced -0.25 by -1/4 = -0.25
rat: replaced 1000000.0 by 1000000/1 = 1000000.0
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced 1500000.0 by 1500000/1 = 1500000.0
rat: replaced 1000000.0 by 1000000/1 = 1000000.0
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced 1000000.0 by 1000000/1 = 1000000.0
rat: replaced 0.5 by 1/2 = 0.5
rat: replaced -0.5 by -1/2 = -0.5
rat: replaced 1000000.0 by 1000000/1 = 1000000.0
rat: replaced 0.5 by 1/2 = 0.5

(%o9)                            [u = 3000000]
(%i10) varR : subst(Au[1], u, variance);
                                                                  2
                 0.5 u             1500000.0     2           0.5 u
(%o10) (- (----------------- + -----------------) ) + --------------------
           0.5 u + 1000000.0   0.5 u + 1000000.0                         2
                                                      (0.5 u + 1000000.0)
                                                           4.5e+12
                                                   + -------------------- = 0.0
                                                                        2
                                                     (0.5 u + 1000000.0)
(%i11) ER : subst(Au[1], u, Ex);
                        0.5 u             1500000.0
(%o11)            ----------------- + ----------------- = 1.2
                  0.5 u + 1000000.0   0.5 u + 1000000.0
(%i12) Er : (% - 1);
                      0.5 u             1500000.0
(%o12)          ----------------- + ----------------- - 1 = 0.2
                0.5 u + 1000000.0   0.5 u + 1000000.0
(%i13)

(a)

revised on 2016-11-05

×10⁶ を M で表す。

雨が降らない場合(if it does not rain)
確率(probability) p₁ = 50%
受取額(amount received) X₁ = 3×10⁶
投資額(amount invested) X₀ = 1×10⁶ + 0.5u
総収益(toral return) R₁ = X₁ / X₀ = 3×10⁶ / (1×10⁶ + 0.5u) = 3M / (1M + 0.5u)

雨が降る場合(if it rains)
確率(probability) p₂ = 50%
受取額(amount received) X₁ = u
投資額(amount invested) X₀ = 1×10⁶ + 0.5u
総収益(toral return) R₂ = X₁ / X₀ = u / (1×10⁶ + 0.5u) = u / (1M + 0.5u)

期待総収益 E(R) = R₁p₁ + R₂p₂
= 0.5(3×10⁶ + u) / (1×10⁶ + 0.5u)
= (1.5×10⁶ + 0.5u) / (1×10⁶ + 0.5u) = (1.5M + 0.5u) / (1M + 0.5u)

次を削除する。(2016-11-05)

投資額 = 100万 + 0.5u($)、期待受取額＝ 0.5 * 300万 + 0.5u($)
期待収益＝ (0.5 * 300万 + 0.5u) / (100万 + 0.5u) = (150万 + 0.5u) / (100万 + 0.5u)

(b)

E(R²) = (0.5R₁² + 0.5R₂²) = 0.5(9×10¹² + u²) / (1×10⁶ + 0.5u)² = (4.5×10¹² + 0.5u²) / (1×10⁶ + 0.5u)²
E(R)² = (1.5×10⁶ + 0.5u)² / (1×10⁶ + 0.5u)² = (2.25×10¹² + 1.5×10⁶u + 0.25u²) / (1×10⁶ + 0.5u)²
分散 v(R) = E(R²) - E(R)²
= (4.5×10¹² + 0.5u²) / (1×10⁶ + 0.5u)² - (2.25×10¹² + 1.5×10⁶u + 0.25u²) / (1×10⁶ + 0.5u)²
= (2.25×10¹² -1.5×10⁶u + 0.25u²) / (1×10⁶ + 0.5u)² = (9×10¹² -6×10⁶u + u²) / (2×10⁶ + u)²
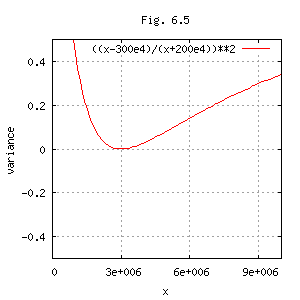
= (u - 3×10⁶)² / (2×10⁶ + u)²
= (u - 3M)² / (u + 2M)²

次を削除する。(2016-11-05)

分散 v = 0.5(300万 / (100万 + 0.5u) - (150万+0.5u) / (100万 + 0.5u))² + 0.5(u / (100万 + 0.5u) - (150万 + 0.5u) / (100万 + 0.5u))²
= 0.5(600万 / (200万 + u) - (300万 + u) / (200万 + u))² + 0.5(2u / (200万 + u) - (300万 + u) / (200万 + u))²
= 0.5((600万 - 300万 - u) / (200万 + u))² + 0.5((2u - 300万 - u) / (200万 + u))²
= 0.5((300万 - u) / (200万 + u))² + 0.5((u - 300万) / (200万 + u))²
= ((u - 300万) / (u + 200万))²

分散のグラフをFig. 6.5に示す。

Fig. 6.5

分散vの導関数(derivative) dv/du を求める。

v = f / g と置き、f/gの導関数を求める。
ただし、f = (u - 3M)², g = (u + 2M)²
f' = 2(u - 3M), g' = 2(u + 2M), g(u)² = (u + 2M)⁴

dv/du
= d(f/g)/du = (f'g - fg') / g(u)² (商の微分法)
= [2(u - 3M)(u + 2M)² - (u - 3M)² * 2(u + 2M)] / (u + 2M)⁴
= [2(u - 3M)(u + 2M) - (u - 3M)² * 2] / (u + 2M)³
= 2(u - 3M)[(u + 2M) - (u - 3M)] / (u + 2M)³
= 2(u - 3M)5M / (u + 2M)³
= 10M(u - 3M) / (u + 2M)³
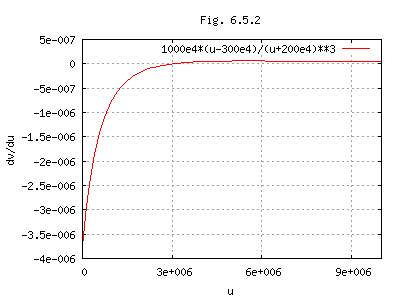
∴ dv/du = 10M(u - 3M) / (u + 2M)³

dv/du = 2(u - 300万) / (u + 200万)((u - 300万) / (u + 200万))'
　(　((u - 300万) / (u + 200万))' = 500万 / (u + 200万)²　)
dv/du = 2(u - 300万) / (u + 200万) * 500万 / (u + 200万) = 1000万(u - 300万) / (u + 200万)³

(dv/duの図をFig. 6.5.2に示す。)(2005-2-16)
dv/du < 0, (0 < u < 3M)
dv/du > 0, (3M < u)

vの増減表をTable 6.5 に示す。(2011-11-03)

Table 6.5
u	0		3M
dv/du		-	0	+
v		↓	minimum	↑

∴ u = 3M の時、分散が最小となる。その分散 v は、v(u = 3M) = 0（$²）。

よって、総収益(total return)の分散(variance)を最小化するためには、 3M 単位の保険を購入すべきである。
期待総収益E(R)(u = 3M) = (1.5M + 0.5 * 3M) / (1M + 0.5 * 3M) = 1.2
期待収益率E(r) = 期待総収益E(R) - 1 = 0.20 = 20%

graph

図化コマンド

図化コマンドを次のリンクに示す。

history

2004-08-08 create.
2005-2-16, 2011-10-26 revise.
2011-10-29 画像ファイルをpngフォーマットに変更した。
2011-11-03 Table 6.5 added.
2016-11-06 (a),(b) revised and solution with Maxima added.
2021-02-17 change XHTML to html5, change shift-jis to utf-8, add viewport.