6.7

(2004-8-13), revised on 2011-10-26, 2011-10-29.
2011-10-29 画像ファイルをpngフォーマットに変更した。

(a)

式(6.5a)は、
2w₁ + w₂ - 0.4λ - μ = 0　(1)
w₁ + 2w₂ + w₃ - 0.8λ - μ = 0　(2)
w₂ + 2w₃ - 0.8λ - μ = 0　(3)
となり、
∴ w₁ = 0.1 λ + 0.5μ　(4)
　w₂ = 0.2 λ　(5)
　w₃ = 0.3 λ + 0.5μ　(6)

式(6.5b)は、
0.4w₁ + 0.8w₂ + 0.8w₃ = r　(7)
となり、
0.4(0.1λ + 0.5μ) + 0.8(0.2λ) + 0.8(0.3λ+0.5μ) = r
∴ 2.2λ + 3μ = r　(8)

式(6.5b)は、
w₁ + w₂ + w₃ = 1
となり、
(0.1λ + 0.5μ) + (0.2λ) + (0.3λ + 0.5μ) = 1
∴ 3λ + 5μ = 5　(9)

式(8)、(9)から、
∴ λ = (25r - 15) / 2　(10)
　μ = (11 - 15r) / 2　(11)

式(4)、(5)、(6)に式(10)、(11)を代入すると、
w₁ = (-5r + 4) / 2　(12)
w₂ = (5r - 3) / 2　(13)
w₃ = 1 / 2　(14)

分散σ² = 2w₁² + 2w₁w₂ + 2w₂² + 2w₂w₃ + 2w₃²
に式(12)、(13)、(14)を代入すると、
σ² = (25 / 2)[(r - 3 / 5)² + 2]

上式を図化したものを Fig.6.7 に示す。

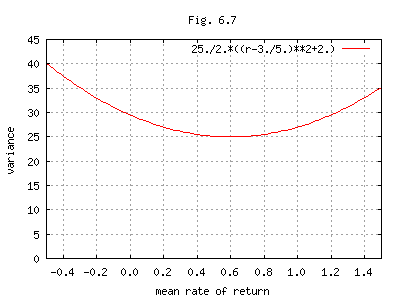
∴ r = 3 / 5の時分散が最小となる。

r = 3 / 5を式(12)、(13)、(14)に代入すると、
w₁ = 0.5
w₂ = 0
w₃ = 0.5
∴ w = (0.5, 0, 0.5)

(b)

式(11)と μ = 0 から、
r = 11 / 15

これを式(12)、(13)、(14)に代入し、
w₁ = 1 / 6
w₂ = 1 / 3
w₃ = 1 / 2
∴ w = (1/6, 1/3, 1/2)

(c)

(2004-08-14修正), revised on 2011-10-29.

図化コマンド

図化コマンドを次のリンクに示す。

• Fig.6.7

history

2004-08-13 create.
2011-10-26 revise.
2011-10-29 画像ファイルをpngフォーマットに変更した。
2021-02-17 change XHTML to html5, change shift-jis to utf-8, add viewport.